
#MATLAB ODE45 HOW TO#
That being said, I can't give you a recommendation about how to better go about applying the constraints you need without understanding more about the problem.

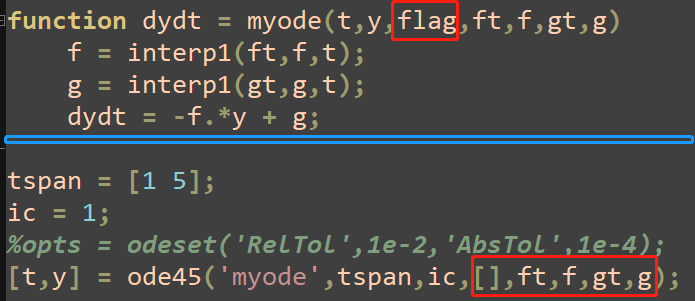
#MATLAB ODE45 CODE#
If what you're trying to do is hardcode behavior for your differential equations at specific t values, it will be quite difficult and I would strongly discourage it any tiny change to your code may affect the t values which the algorithm uses and the endeavor will be for naught. For this problem, we will use the ode45 solver which uses a Runge-Kutta iterative method to achieve 4 th and 5 th order accuracy. The selection of the appropriate solver is dependent on the type of ODE you are solving and the desired accuracy. To be valid, the call must name the function ( f ) defined in MATLAB®, and specify both the time range ( Trange ) and the initial condition vector ( IC ). MATLAB has many ODE solvers available for the coder. In general, u can be designed as a linear feedback control law, such as u Kx, where K is a 50-by-50 matrix.Let me give you a simpler example here. The ode15s command uses MATLAB® to compute the ODE15S solution of a differential system. In order to solve an ODE using ode45, you need to first define the function to describe the complete dynamics.In the linear state space system you provided, the definition of u is missing.

Combining these two things, what you end up with are somewhat confusing t values in the ode45 output and many more calls to your function than you may expect. The ode45 command uses MATLAB® to compute the ODE45 solution of a differential system. The basic command to call the ode45 integrator looks like this: t,state ode45(dstate,time,ICs,options) The integrator takes a vector of initial conditions (either a column or row vector) and integrates it using the dynamics given in the dstate function. From what I can gather from your descripion and the ODE45 Matlab page is that the difference between the time values might come from the way the solver works IF you provide it a tspan vector longer than two: 'If tspan has more than two elements t0,t1,t2.,tf, then the solver returns the solution evaluated at the given points. What this means for you is that your function will get called at many more points than what ode45 shows in its final results because of how this algorithm works. ode45.m MATLAB’s pre-built ode45.m integrator is generally the best option. Second, ode45 uses a method of numerical integration called Runge-Kutta. Matlab: ode45 and 4-th order Runge-Kutta method yield different values 2 Solving 3 coupled nonlinear differential equations using 4th order Runge Kutta in. TWo important things to understand about ode45 are that, first, it's an adaptive step-size numerical integrator, which means it will intelligently choose the t values to most efficiently integrate your function. I'm not sure I completely understand, but here's what I think might be going on. $$h = \left(\frac$ produces the following results using ode45(.Could you be more specific, and maybe include some code with outputs for your ode45 call and "checking" you're doing in the function? Specify a single output to return a structure containing information about the solution, such as the solver and evaluation points. The function vdp1.m ships with MATLAB and encodes the equations. Let's first take your equation for $h$, which is defined as: Solve the van der Pol equation with 1 using ode45.


 0 kommentar(er)
0 kommentar(er)
